问题
填空题
设α=(1，0，1)T，A=ααT，若B=(kE+A)*是正定矩阵，则k的取值范围是______．
答案
参考答案：k＜-2或k＞0
解析： 由于
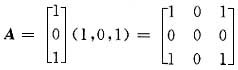
有|λE-A|=λ3-2λ2=λ2(λ-2)
即矩阵A的特征值是2，0，0，从而矩阵KE+A的特征值是k+2，k，k，那么B的特征值是k2，k(k+2)，k(k+2)．
所以，B正定的充要条件是：k2＞0，k(k+2)＞0，得k＜-2或k＞0．
由A对称
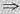kE+A对称；若A对称可逆
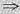A-1对称可逆
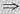A*对称可逆．
所以本题矩阵B是对称矩阵，进而可讨论正定问题．