从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
My son lives in a big city in France. People there are very busy. There are many supermarkets and
1 on the streets. It is very easy to go
2 . You can buy a lot of nice things there. My son works in a restaurant. He
3 Chinese food there. There is a big cinema (电影院) near my son’s home
4 he often goes to the movies. Life in the city is colorful. There are a lot of
5 of interest to visit. Also, it is easy for them to take a bus to
6 other cities from theirs.
I like country (乡村) life best. That’s
7 I don’t like to live in the city with my son. Here, in the country, I can
8 the fields (田地) and plants. Sometimes some little animals
9 in my garden. I think it’s very
10 to be in this kind of quiet and fun place.
| 小题1: | | A.hospitals | B.restaurants | C.shops | D.banks |
|
| 小题2: | | A.running | B.swimming | C.shopping | D.sleeping |
|
| 小题3: | | A.takes | B.sees | C.finds | D.cooks |
|
| 小题5: | | A.rooms | B.cities | C.places | D.countries |
|
| 小题6: | | A.get to | B.look for | C.wait for | D.talk about |
|
| 小题9: | | A.play | B.study | C.read | D.sing |
|
| 小题10: | | A.boring | B.scary | C.exciting | D.relaxing |
|
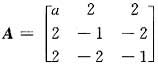 的伴随矩阵A*的特征向量,其中r(A*)=3,则a=______.
的伴随矩阵A*的特征向量,其中r(A*)=3,则a=______.

