问题
填空题
设A是三阶实对称矩阵,存在正交阵Q=[ξ1,ξ2,ξ3],使得Q-1AQ=QTAQ=
 ,则矩阵B=A-ξ1
,则矩阵B=A-ξ1
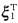 的特征值是______.
的特征值是______.
答案
参考答案:0,2,3
解析: 由题设条件知,A有特征值λ1=1,λ2=2,λ3=3,对应的特征向量分别是ξ1,ξ2,ξ3,即有Aξi=λiξi=iξi,i=1,2,3
又Q是正交矩阵,ξ1,ξ2,ξ3满足条件
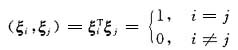
故
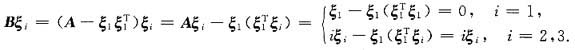
故A-ξ1
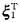 有特征值0,2,3.
有特征值0,2,3.
设A是三阶实对称矩阵,存在正交阵Q=[ξ1,ξ2,ξ3],使得Q-1AQ=QTAQ=
 ,则矩阵B=A-ξ1
,则矩阵B=A-ξ1
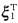 的特征值是______.
的特征值是______.
参考答案:0,2,3
解析: 由题设条件知,A有特征值λ1=1,λ2=2,λ3=3,对应的特征向量分别是ξ1,ξ2,ξ3,即有Aξi=λiξi=iξi,i=1,2,3
又Q是正交矩阵,ξ1,ξ2,ξ3满足条件
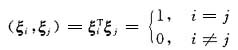
故
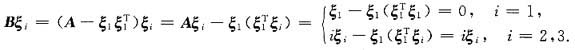
故A-ξ1
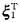 有特征值0,2,3.
有特征值0,2,3.