问题
问答题
设X,Y是两个离散型随机变量,X只取-1和1两个值,Y只取-1,0,1三个值,已知EX=0.2,
EY=0.25,PX=-1,Y=1=0.2,PX=1,Y=-1=0.1,PY=-1=0.2.试求:
(Ⅰ) X与Y的联合概率分布与它们的协方差;
(Ⅱ) X与Y2的联合概率分布与它们的协方差.
答案
参考答案:[解] (Ⅰ)首先我们列出X与Y的联合概率分布结构表(见表1),表中未知的Pij待求.
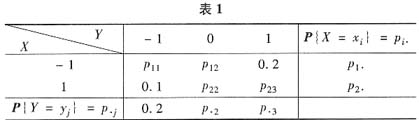
根据联合分布与边缘分布间的关系及数学期望定义容易求出表1中pij(i=1,2,j=1,2,3)各值,对照表1,具体计算如下:

从上述计算结果可得X与Y的联合概率分布(见表2)为
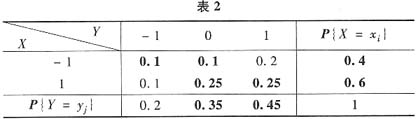
EXY=(-1)(-1)×0.1+(-1)×1×0.2+1×(-1)×0.1+1×1×0.25=0.05,
于是 COV(X,Y)=EXY-EXEY=0.05-0.2×0.25=0.
(Ⅱ)从X与Y的联合概率分布容易求出X与Y2的联合概率分布、边缘分布(见表3).
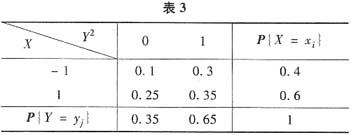
EX=0.2,EY2=0.65,EXY2=0.05,
于是 cov(X,Y2)=EXY2-EXEY2=0.05-0.2×0.65=-0.08.
