问题
问答题
设f(x)在[0,1]连续,在(0,1)可导,且f(0)=0,f(1)=1,求证:
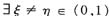 使得
使得
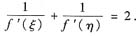
答案
参考答案:[证明] 因为
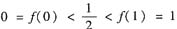 ,由连续函数的介值定理可知存在c∈(0,1),使得
,由连续函数的介值定理可知存在c∈(0,1),使得
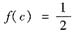
对此c,在[0,c]与[c,1]上分别应用拉格朗日中值定理
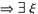 ∈(0,c),η∈(c,1),使得
∈(0,c),η∈(c,1),使得
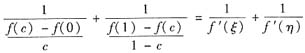
又左端为
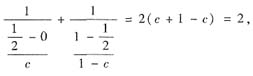
故得证.
解析: 按题设与要证的结论,要在[0,1]的某两个区间上用拉格朗日中值定理:
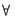 取c∈(0,1),分别在[0,c]与[c,1]上用拉格朗日中值定理
取c∈(0,1),分别在[0,c]与[c,1]上用拉格朗日中值定理
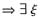 ∈(0,c),η∈(c,1)使得
∈(0,c),η∈(c,1)使得
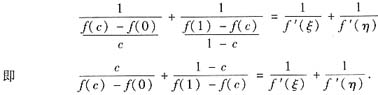
关键是取c∈(0,1)及f(C)使得左端为2,只需取f(C)使得

则达目的.
