问题
解答题
(1)求一次函y=2x-2的图象l1与y=
(2)求直线l1与y轴交点A的坐标;求直线l2与x轴的交点B的坐标; (3)求由三点P、A、B围成的三角形的面积. |
答案
(1)由
解得:y=2x-2 y=
x-11 2
所以点P的坐标为(x= 2 3 y=- 2 3
,-2 3
),2 3
(2)当x=0时,由y=2×0-2=-2,所以点A坐标是(0,-2).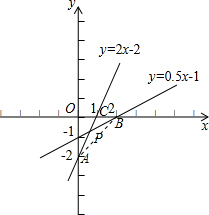
当y=0时,由0=-
x-1,得x=2,所以点B坐标是(2,0).1 2
(3)如图:连AB,
∴S△PAB=S△ABC-S△PBC=
×2×1-1 2
×1 2
×1=2 3
.2 3
