问题
问答题
设f(x)在[0，1]连续，在(0，1)可导，且f(0)＜0，f(1)＜1，
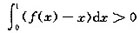求证：至少
一点ξ∈(0，1)，使得f’(ξ)+ξ2(f(ξ)-ξ)=1．
答案
参考答案：
[分析]： 即证明
[*]
由此，只需研究[*]在[0，1]或[0，1]内的某个闭区间上是否满足罗尔定理的条件．函数F(x)在这样的闭区间上连续，开区间内可导是明显的，从而关键是验证函数F(x)在[0，1]内某两点函数值相等，为此又只须验证函数[*]上某两点处取值为零．
[证明] g(0)=f(Q)＜0，g(1)=f(1)-1＜0
[*]
即 g(η)=f(η)-η＞0
[*]
在[ξ1，ξ2]上可对F(x)用罗尔定理[*]，即
f’(ξ)+ξ2(f(ξ)-ξ)=1．