问题
问答题
设u=f(x,y,z)有连续的一阶偏导数,又函数y=y(x)及z=z(x)分别由下列两式确定:

求
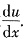
答案
参考答案:在exy-xy=2两边取微分,得
exy(ydx+xdy)-(ydx+xdy)=0,即(xexy-x)dy=(y-yexy)dx,从而
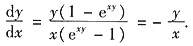 ①
①
在
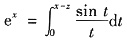 两边取微分,得
两边取微分,得
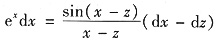 ,即
,即
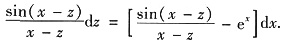
从而
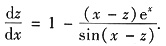 ②
②
又
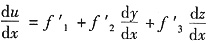 ,将式①,②代入,得
,将式①,②代入,得
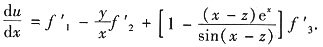
解析:[考点] 多元函数偏导数及隐函数求导
