问题
问答题
已知f(x)在[1,2]连续,(1,2)可导,且f(1)=0,f(2)=1.
试证:
存在两个不同点η,ζ∈(1,2)使f′(η)f′(ζ)=1.
答案
参考答案:在[1,ξ],[ξ,2]上分别对f(x)用拉格朗日中值定理,存在η∈(1,ξ),ζ∈(ξ,2),故η≠ζ且η,ζ∈(1,2),使

从而
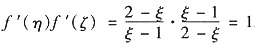 .
.
解析:[考点] 闭区间连续函数性质与微分中值定理
已知f(x)在[1,2]连续,(1,2)可导,且f(1)=0,f(2)=1.
试证:
存在两个不同点η,ζ∈(1,2)使f′(η)f′(ζ)=1.
参考答案:在[1,ξ],[ξ,2]上分别对f(x)用拉格朗日中值定理,存在η∈(1,ξ),ζ∈(ξ,2),故η≠ζ且η,ζ∈(1,2),使

从而
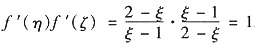 .
.
解析:[考点] 闭区间连续函数性质与微分中值定理