问题
问答题
设f(x)在[a,b]上可导,且f’(x)≤M,f(a)=0,证明:
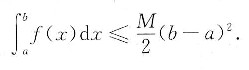
答案
参考答案:由题设,对[*]x∈[a,b],可知f(x)在[a,b]上满足拉氏微分中值定理,于是有
f(x)=f(x)-f(a)=f’(ξ)(x-a),ξ∈(a,x).
因为f’(x)≤M,所以f(x)≤M(x-a).由定积分比较定理,有
[*]
解析:[考点提示] 定积分的证明.
设f(x)在[a,b]上可导,且f’(x)≤M,f(a)=0,证明:
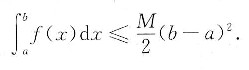
参考答案:由题设,对[*]x∈[a,b],可知f(x)在[a,b]上满足拉氏微分中值定理,于是有
f(x)=f(x)-f(a)=f’(ξ)(x-a),ξ∈(a,x).
因为f’(x)≤M,所以f(x)≤M(x-a).由定积分比较定理,有
[*]
解析:[考点提示] 定积分的证明.