问题
问答题
设u=u(x，t)有二阶连续偏导数，并满足
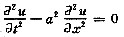
其中a＞0为常数．
(Ⅰ)作自变量代换
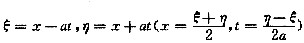，导出u对x与y的一、二阶偏导数与u对ξ，η的一、二阶偏导数的关系式．
(Ⅱ)导出u作为ξ，η的函数的二阶偏导数所满足的方程．
(Ⅲ)求u(x，t)．
答案
参考答案：[分析与求解] (Ⅰ)由复合函数求导法得
[*]
[*]
(Ⅱ)由(Ⅰ)中的①，②式得
[*]
即[*]
(Ⅲ)把③式写成
[*]
[*]是连续可微的任意函数，再对ξ积分一次，并注意到积分常数可依赖η，于是得
u=f(ξ)+g(η)
其中f(ξ)和g(η)是二次连续可微的[*]函数，回到变量x，t得
u(x，t)=f(x-at)+g(x+at)．