问题
问答题
已知非齐次方程组
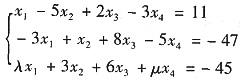
有三个线性无关的解.
证明：方程组系数矩阵A的秩r(A)=2；
答案
参考答案：设α1，α2，α3是方程组AX=b的3个线性无关的解，则α1-α2，α1-α3是其导出组AX=0的两个线性无关的解，于是4-r(A)≥2，即有r(A)≤2.
又A中存在2阶子式，例如
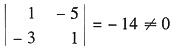，有r(A)≥2，从而得r(A)=2.
搜题请搜索小程序“爱下问搜题”
已知非齐次方程组
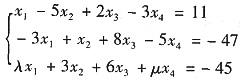
有三个线性无关的解.
证明：方程组系数矩阵A的秩r(A)=2；
参考答案：设α1，α2，α3是方程组AX=b的3个线性无关的解，则α1-α2，α1-α3是其导出组AX=0的两个线性无关的解，于是4-r(A)≥2，即有r(A)≤2.
又A中存在2阶子式，例如
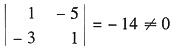，有r(A)≥2，从而得r(A)=2.