问题
问答题
设3阶矩阵A的特征值为λ1=1，λ2=2，λ3=3，对应的特征值向量依次为：
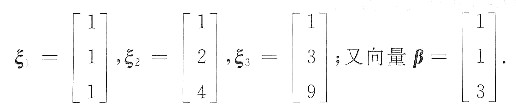
(1)设β用ξ1，ξ2，ξ3线性表示；
(2)求Anβ(n为自然数)．
答案
参考答案：(1) 设β=x1ξ1+x2ξ2+x3ξ3，对增广矩阵(α1，α2，α3，β)作初等行变换，有
[*]
解出：x3=1，x2=-2，x1=2．故β=2ξ1-2ξ2+ξ3．
(2) 由Aξi=λiξi得Anξi=[*](i=1，2，3)．据(1)结论，β=2ξ1-2ξ2+ξ3，则有
Aβ=A(2ξ1-2ξ2+ξ3)=2Aξ1-2Aξ2+Aξ3．
于是
[*]
[*]
解析：[考点提示] 矩阵特征值特征向量的逆问题．