问题
问答题
已知二次型f(x1，x2，x3)=XTAX在正交变换X=QY，下的标准形为-y21-y22，且Q的第三列为
．
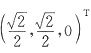证明A-E为负定矩阵，其中E为三阶单位矩阵．
答案
参考答案：由于矩阵A的特征值为-1，-1，0，那么A-E的特征值为-2，-2，-1，因为A-E的特征值全部小于0，所以A=E负定．
搜题请搜索小程序“爱下问搜题”
已知二次型f(x1，x2，x3)=XTAX在正交变换X=QY，下的标准形为-y21-y22，且Q的第三列为
．
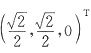证明A-E为负定矩阵，其中E为三阶单位矩阵．
参考答案：由于矩阵A的特征值为-1，-1，0，那么A-E的特征值为-2，-2，-1，因为A-E的特征值全部小于0，所以A=E负定．