设函数y=f(x)在(-∞，+∞)内可导，且对任意实数a，b均满足f(a+6)=ea

问题问答题

设函数y=f(x)在(-∞，+∞)内可导，且对任意实数a，b均满足f(a+6)=e^af(6)+e^bf(a)，又f^’(0)=1，试求f(x)及f^’(x)．

答案

参考答案：由于对任意a，b，等式f(a+b)=e^af(b)+e^bf(a)均成立，故建立微分方程．根据导数的定义，利用导数的定义式f(x+Δx)展开．

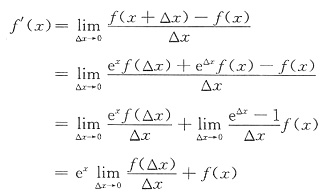令a=b=0，由f(a+b)=e^af(b)+e^bf(a)得，f(0)=0，又f^’(0)=1故f^’(x)=e^xf^’(0)+f(x)=e^x+f(x)即f(x)的微分方程为f^’(x)-f(x)=e^x，f(0)=0两边乘e^-x，得(e^-xf(x))^’=1，两边积分，得

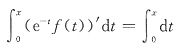故f(x)=xe^x，f^’(x)=e^x+xe^x=(x+1)e^x．