设a1=(1，2，-1，0)T，a2=(1，1，0，2)T，a3=(2，1，1，a)

问题填空题

设a₁=(1，2，-1，0)^T，a₂=(1，1，0，2)^T，a₃=(2，1，1，a)^T，若有a₁，a₂，a₃生成的向量空间维数为3，则a应满足______．

答案

参考答案：a≠6

解析：由a₁，a₂，a₃所生成的向量空间的维数是3，可知向量组的秩r(a₁，a₂，a₃)=3，那么对(a₁，a₂，a₃)做初等变换，有

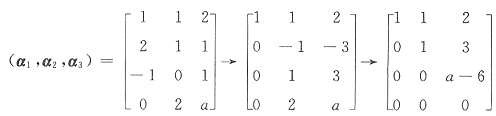，由于r(a₁，a₂，a₃)=3，所以a-6≠0，即a≠6．