问题
单项选择题
已知方程x3+2x2-5x-6=0的根为x1=-1，x2，x3，则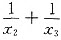
=（）。
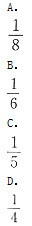
A.A
B.B
C.C
D.D
答案
参考答案：B
解析：
[方法一] 将x3+2x2-5x-6分解因式，得
(x3+x2)+(x2-5x-6)=x2(x+1)+(x+1)(x-6)
=(x+1)(x2+x-6)=(x+1)(x+3)(x-2)
不妨令x2=-3，x3=2，所以
。选B。
[方法二] 利用竖式长除法。
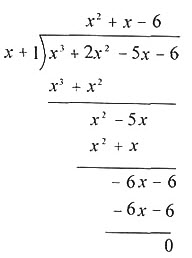
则有(x+1)(x2+x-6)=0
对于x2+x-6=0也可由韦达定理得x2+x3=-1，x2x3=-6。
所以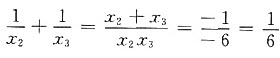
。选B。