问题
问答题
设有抛物线y=x2-(α+β)x+αβ(α<β),已知该抛物线与y轴的正半轴及x轴所围图形面积A1等于这条抛物线与x轴所围图形的面积A2,求实数α,β之间的关系。
答案
参考答案:
依题意抛物线开口向上,二个实根为α和β,为了使面积A1存在,抛物线应与y轴正半轴相交,则
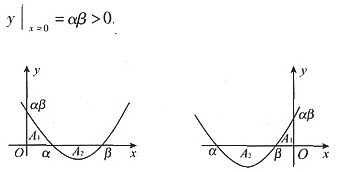
当α>0,β>α>0时,由于A1=A2,一个图形在x轴上方,另一个在x轴下方,应有
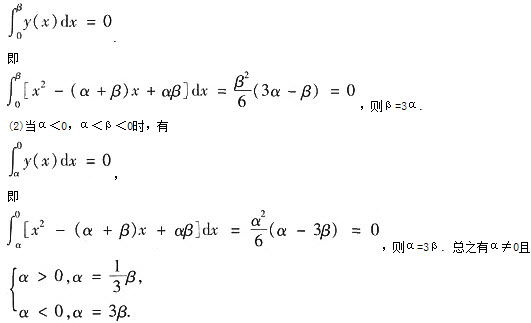
解析:
[考点] 定积分的几何意义
设有抛物线y=x2-(α+β)x+αβ(α<β),已知该抛物线与y轴的正半轴及x轴所围图形面积A1等于这条抛物线与x轴所围图形的面积A2,求实数α,β之间的关系。
参考答案:
依题意抛物线开口向上,二个实根为α和β,为了使面积A1存在,抛物线应与y轴正半轴相交,则

当α>0,β>α>0时,由于A1=A2,一个图形在x轴上方,另一个在x轴下方,应有
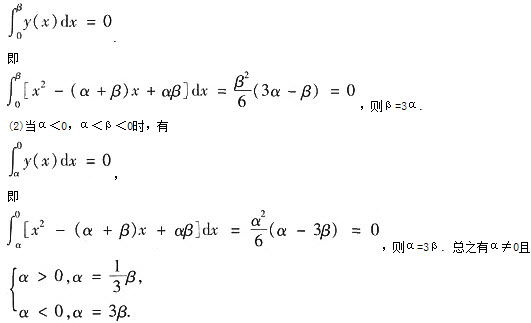
解析:
[考点] 定积分的几何意义