问题
问答题
设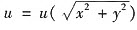 具有连续的二阶偏导数,且满足
具有连续的二阶偏导数,且满足
试求函数u的表达式。
答案
参考答案:
令

相应的齐次方程的特征方程为λ2+1=0,λ=±i,方程(*)相应的齐次方程的通解为U=c1cos r+c2sin r.
由于非齐次项f(r)=r2e0,而0非特征值,故非齐次方程有特解形如u*=Ar2+Br+D.
代入方程(*)后,得u*=r2-2(即A=1,B=0,D=-2),方程(*)通解为u=U+u*=c1cos r+c2sin r+r2-2.
从而所求的函数为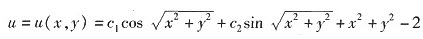 (c1,c2为任意常数).
(c1,c2为任意常数).
解析:
[考点] 二阶常系数线性非齐次微分方程
