参考答案：

记f(x)=e^x+x²-3x-4在(-∞，+∞)连续、可导. f(0)=-3＜0，f(2)=e²-6＞0. 在闭区间[0，2]上对f(x)用连续函数零值定理，可知f(x)在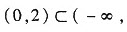+∞)内至少有一零点. 即方程至少有一实根，

下面反证实根不能超过三个. 设不然，存在互异x₁，x₂，x₃，x₄使f(x_i)=0(i=1，2，3，4). 分别在[x₁，x₂]，[x₂，x₃]，[x₃，x₄]上对f(x)用罗尔定理，f′(x)应该有三个根，但f′(x)=e^x+2x-3；f″(x)=e^x+2 ＞0，表明f′(x)在(-∞，+∞)严格单调增加，最多有一个实根与f′(x)有三个实根矛盾.

故f(x)的零点，即方程e^x=x²+3x+4的实根，不能超过三个.

解析：

[考点] 导数应用