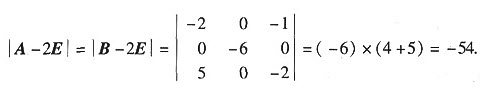问题
填空题
已知矩阵A与B相似，而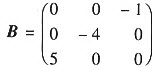
，则行列式|A-2E|=（）。
答案
参考答案：-54
解析：
[考点] 行列式的计算
由于A～B，即存在可逆矩阵P，使P-1AP=B，当k为任意实数时，
P-1(A+kE)P=P-1AP+P-1(kE)P=B+kE.
即A+kE～B+kE，相似矩阵有相同的行式，故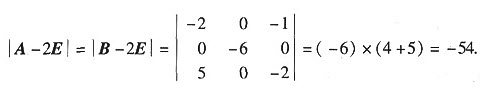
搜题请搜索小程序“爱下问搜题”
已知矩阵A与B相似，而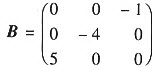，则行列式|A-2E|=（）。
参考答案：-54
解析：
[考点] 行列式的计算
由于A～B，即存在可逆矩阵P，使P-1AP=B，当k为任意实数时，
P-1(A+kE)P=P-1AP+P-1(kE)P=B+kE.
即A+kE～B+kE，相似矩阵有相同的行式，故