问题
单项选择题
设连续型随机变量X1,X2相互独立,分布函数分别为F1(x),F2(x),概率密度分别为f1(x),f2(x),则随机变量min(X1,X2)的概率密度为()。
A.f1(x)f2(x)
B.f1(x)+f2(x)
C.f1(x)F2(x)+f2(x)F1(x)
D.f1(x)(1-F2(x))+f2(x)(1-F1(x))
答案
参考答案:D
解析:
[考点] 连续型随机变量的分布函数与概率密度
对任意实数x,将min(X1,X2)的分布函数记为F(x),则
F(x)=P(min(X1,X2)≤X)=1-P(min(X1,X2)>X)
=1-P(X1>x)P(X2>x)
=1-[1-F1(x)][1-F2(x)],
于是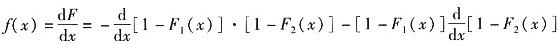
=f1(x)(1-F2(x)+f2(x)[1-F1(x)]. 选D.
