问题
问答题
某家庭准备以抵押贷款方式购买一套住房。该家庭月总收入7000元，最多能以月总收入的25%支付住房贷款的月还款额。年贷款利率为6%，最长贷款期限20年，最低首付款为房价的30%，若采用按月等额偿还方式，问：
（1）该家庭能购买住房的最高总价是多少若第5年年末银行贷款利率上调为9%，为保持原月偿还额不变，则：
（2）该家庭需在第6年年初一次性提前偿还贷款多少元？
（3）如果不提前偿还贷款，则需将贷款期限延长多少年？
答案
参考答案：
(1)依题意，该家庭的月还款额A=7000×25%=1750(元)
月贷款利率i=6%÷12=0.5%
计息期n=20×12=240
则有偿还能力的最大抵押贷款额
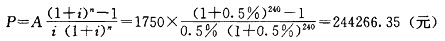
该家庭购房最高总价：244266.35÷(1-30%)＝348951.93(元)=34.90(万元)
(2)第5年年末剩余贷款额，即后15年每月还款额1750元在第5年年末的现值
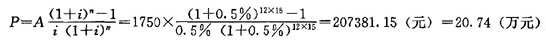
第5年年末银行贷款利率上调为9%(月利率0.75%)，后15年每月还款额1750元在第5年年年末的现值为：
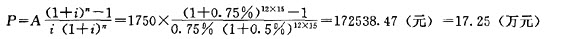
因此，该家庭需在第6年年初一次性提前偿还贷款：20.74-17.25=3.49(万元)
(3)若不提前还贷，月还款额不变，今后n月需还第5年年末时的剩余贷款额20.74万元，则：
由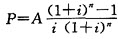
即207381.15=1750×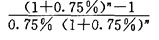
可得出：(1+0.75%)n＝8.9909，两边取对数可求得n
n=293.93(月)
因此，还款年限将延长：293.93÷12-15=9.49(年)