问题
单项选择题
设A为三阶矩阵,ξ1=(1,2,-2)T,ξ2=(2,1,-1)T,ξ3=(1,1,t)T是非齐次线性方程组AX=b的解向量,其中b=(1,3,-2)T,则()。
A.t=-1,必有r(A)=1
B.t=-1,必有r(A)=2
C.t≠-1,必有r(A)=1
D.t≠-1,必有r(A)=2
答案
参考答案:C
解析:
[考点] 非齐次线性方程组
方法一 记B=(ξ1,ξ2,ξ3)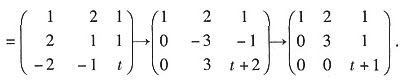
当t≠-1时,r(B)=3,ξ1,ξ2,ξ3为AX=b的三个线性无关的解,故ξ1-ξ2,ξ1-ξ3为其导出组AX=0的两个线性无关的解,从而3-r(A)≥2,即r(A)≤1,但A≠O(如果A=O,则AX≠b,方程组AX=b无解,矛盾). 故r(A)≥1,于是r(A)=1. 选C.
方法二 记B=(ξ1,ξ2,ξ3),则AB=(Aξ1,Aξ2,Aξ3)=(b,b,b). 当t≠-1时,r(B)=3. 于是r(A)=r(AB)=r(b,b,b)=1. 选C.
