问题
单项选择题
A是3阶矩阵且AX=0有通解：k1α1+k2α2(k1，k2为任意常数)，又知Aα3=α3，P是三阶可逆矩阵，使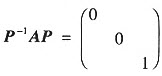
，则P应该是（）。
A．(α1，α2，α1+α3)
B．(α2，α3，α1)
C．(α1+α2，-α2，2α3)
D．(α1+α2，α2+α3，α3)
答案
参考答案：C
解析：
[考点] 矩阵相似对角化
AX=0有通解k1α1+k2α2表明α1，α2是矩阵A对应二重特征值λ1=λ2=0的线性无关的特征向量. 而Aα3=α3指出α3是A属于特征值λ3=1的特征向量，注意到k1α1+k2α2(k1，k2不同时为0)仍是A属于λ1=λ2=0的特征向量；A属于不同特征值λ1(=λ2)≠λ3的特征向量之和不再是A的特征向量；可逆矩阵P中特征向量排序与对角矩阵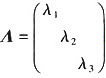
的排序应一致，因此，α1+α2，-α2都是A属于λ1=λ2=0的特征向量，2α3是A属于λ3=1的特征向量，故P=(α1+α2，-α2，2α3). 应选C.
A．中α1+α3不是特征向量；D中α2+α3不是特征向量. B中α3，α1与对应特征值顺序不一致.