问题
问答题
某三轮车厂每生产一付车架要搭配三付轮胎，设轮胎的数量为x，价格为p1，车架的数量为y，价格为p2，又设需求函数x=63-0.25p1与y=60-
p2，成本函数为
C(x，y)=x2+xy+y2+90．求该厂获最大利润时的产量与价格．
答案
参考答案：由需求函数，可得
p1=252-4x，p2=180-3y．则利润函数为
π=xp1+yp2-C(x，y)=x(252-4x)+y(180-3y)-x2-xy-y2-90
=252x-5x2+180y-4y2-xy-90．
约束条件是x=3y，所以拉格朗日函数是
L=252x-5x2+180y-4y2-xy-90-λ(x-3y)．为求极大值，先求偏导数：
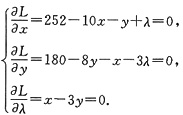
消去λ，则有936-31x-11y=0，再代入x=3y，消去x，得936-104y=0．从而y=9，x=3y=27，这就是获最大利润时的产量．其相应价格为
p1=252-4×27=144，p2=180-3×9=153．
解析： 使用拉格朗日乘数法求之．