问题
问答题
已知产品某项指标X服从拉普拉斯分布，其密度为
f(x)=
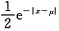，-∞＜x＜+∞，其中μ为未知参数．现从该产品中随机抽取3个，测得其该项指标值为1028，968，1007．
试用最大似然估计法求μ的估计
答案
参考答案：似然函数为
，
．
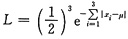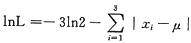要使lnL最大，只需
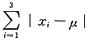最小．记
l=
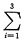|xi-μ|-|1028-μ|+|1968-μ|+|1007-μ|．
当μ≤968时，l=(1028-μ)+(968-μ)+(1007-μ)
=3(1001-μ)≥3(1001-968)=99；
当μ≥1028时，l=(μ-1028)+(μ-968)+(μ-1007)
=3(μ-1001)≥3(1028-1001)=81；
当968＜μ＜1028时，
l=(1028-μ)+(μ-968)+|1007-μ|=60+|1007-μ|．
故当
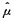=1007时，l最小，取值60．最大似然估计值
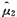=1007．
解析： 待估参数只有一个，可用一阶矩进行估计．