有四张卡片(背面完全相同),分别写有数字1、2、﹣1、﹣2,把它们背面朝上洗匀后,甲同学抽取一张记下这个数字后放回洗匀,乙同学再从中抽出一张,记下这个数字,用字母b、c分别表示甲、乙两同学抽出的数字.
(1)用列表法求关于x的方程x2+bx+c=0有实数解的概率;
(2)求(1)中方程有两个相等实数解的概率.
:解:(1)列表得:
| (1,﹣2) | (2,﹣2) | (﹣1,﹣2) | (﹣2,﹣2) |
| (1,﹣1) | (2,﹣1) | (﹣1,﹣1) | (﹣2,﹣1) |
| (1,2) | (2,2) | (﹣1,2) | (﹣2,2) |
| (1,1) | (2,1) | (﹣1,1) | (﹣2,1) |
∵关于x的方程x2+bx+c=0有实数解,即 b2﹣4c≥0,
∴关于x的方程x2+bx+c=0有实数解的有(1,﹣1),(1,﹣2),(2,1),(2,﹣1),(2,﹣2),(﹣1,﹣1),(﹣1,﹣2),(﹣2,1),(﹣2,﹣1),(﹣2,﹣2)共10种情况,
∴关于x的方程x2+bx+c=0有实数解的概率为: =
=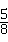 ;
;
(2)(1)中方程有两个相等实数解的有(﹣2,1),(2,1),
∴(1)中方程有两个相等实数解的概率为: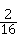 =
=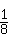 .
.
:(1)根据题意列表,然后根据表格求得所有等可能的结果与关于x的方程x2+bx+c=0有实数解的情况数,根据即可概率公式求解;
(2)首先求得(1)中方程有两个相等实数解的情况,然后即可根据概率公式求解.

