问题
解答题
（12分）将一颗骰子先后抛掷2次，观察向上的点数，求：
（1）两数之和为6的概率；
（2）两数之积是6的倍数的概率；
（3）以第一次向上点数为横坐标x，第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率。
答案
（1）
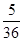；（2）
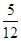；（3）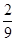
；
题目分析：（1）先后抛掷2次骰子，每次出现1,2,3,4,5,6点的概率都是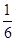
，两数之和的情况有
，
，
，
，
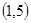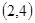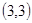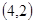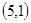；共5钟情况，所以概率为
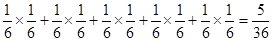。（2）两数之积是6的倍数的有6,12,18,24,30,36；积为6的情况有
，
，
，
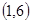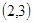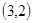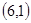两种概率为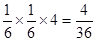
，积为12的情况有
，
，
，
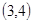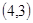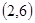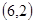两种概率为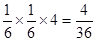，积为18的情况有
，
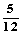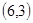两种概率为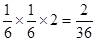
，积为24的情况有
，
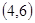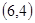两种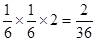，积为30的情况有
，
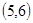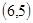两种概率为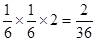，积为36的情况有
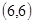一种概率为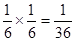
，所以两数之积是6的倍数的概率为
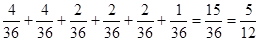。（3）在圆
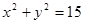的内部，即要满足
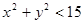，所以有当
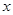取1，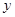
对应可取1,2,3；当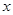取2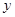，对应可取1,2,3；当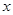取3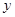，对应可取1,2；所以概率为
。
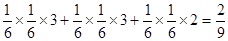试题解析：解：（1）两数之和为6的概率为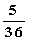
。
（2）此问题中含有36个等可能基本事件，记“向上的两数之积是6的倍数”为事件A，则由下面的列表可知，事件A中含有其中的15个等可能基本事件，所以P(A)=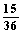 
=,
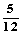所以两数之积是6的倍数的概率为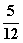
。
此问题共含36个等可能基本事件，而点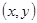
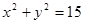在圆的内部有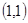
，
，
，
，，，
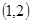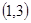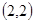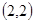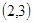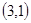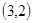，共8种，所以概率为
。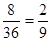