问题
问答题
设f(x,y)在点(0,0)处连续,且
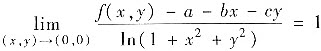 ,其中a,b,c为常数.
,其中a,b,c为常数.
(Ⅰ)讨论f(x,y)在点(0,0)处是否可微,若可微并求出
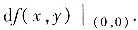
(Ⅱ)讨论f(x,y)在点(0,0)处是否取极值,说明理由.
答案
参考答案:
(Ⅰ)当(x,y)→(0,0)时ln(1+x2+y2)~x2+y2,由求极限中等价无穷小因子替换得
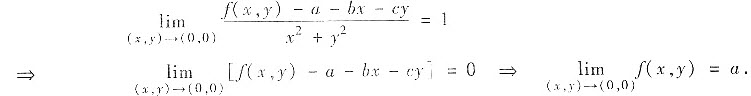
又由f(x,y)在点(0,0)处的连续性即得
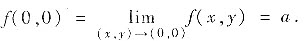
再由极限与无穷小的关系可知
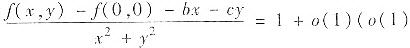 为当(x,y) →(0,0)时的无穷小量)
为当(x,y) →(0,0)时的无穷小量)
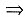
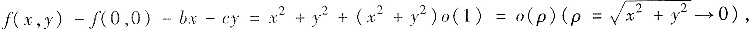
即f(x,y)-f(0,0)=bx+cy+o(ρ)(ρ→0).
由可微性概念
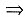 (x,y)在点(0,0)处可微且
(x,y)在点(0,0)处可微且
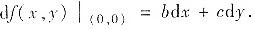
(Ⅱ)由
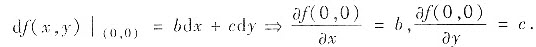 于是当b,c不同时为零时f(x,y)在点(0,0)处不取极值.
于是当b,c不同时为零时f(x,y)在点(0,0)处不取极值.
当b=c=0时,由于
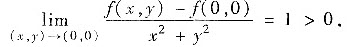
又由极限不等式性质
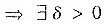 ,当0<x2+y2<δ2时,
,当0<x2+y2<δ2时,
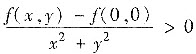 即f(x,y)>f(0,0).
即f(x,y)>f(0,0).
因此,f(x,y)在点(0,0)处取极小值.
解析:
本题有如下变式,题(Ⅰ)不变,题(Ⅱ)改为:求面积z=f(x,y)在点M0(0,0,f(0,0))处的切面方程.
解:曲面z=f(x,y)在点M0(0,0,f(0,0))=(0,0,a)处的切面方程是
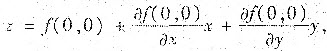
即z=a+bx+cy.
