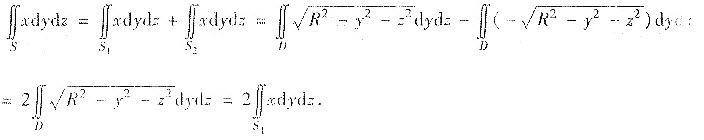问题
单项选择题
设S为球面：x2+y2+z2=R2，则下列同一组的两个积分均为零的是（）
A．
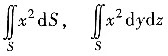
B．
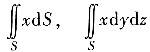
C．
D．
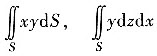
答案
参考答案：C
解析：
注意第一类曲面积分有与三重积分类似的对称性质.
因S关于yz平面对称，被积函数x与xy关于x为奇函数
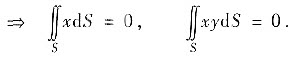
被积函数x2关于x为偶函数
特别要注意，第二类曲面积分有与三重积分不同的对称性质：
因S关于yz平面对称，被积函数x2对x为偶函数
被积函数x对x为奇函数
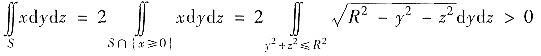(这里设S取外侧).
类似可得
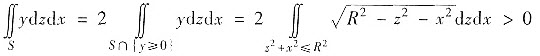(这里仍设S取外侧).
由上分析可知，
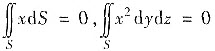，因此应选C.
评注：设S取外侧，记S1，S2分别为前、后半球，于是S1，S2分别取前侧与后侧
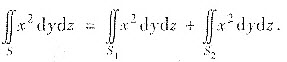
S在yz平面的投影区域为D：y2+z2≤R2
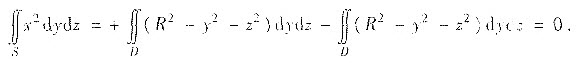
同理
