参考答案：

(Ⅰ)由于A^Cα=CAα-BA^Bα，故

A^Dα=CA^Bα-BA^Cα=CA^Bα-B(CAα-BA^Bα)=GA^Bα-FAα.

若k_Aα+k_BAα+k_CA^Dα=0，即k_Aα+k_BAα+k_C(GA^Bα-FAα)=0,

亦即k_Aα+(k_B-Fk_C)Aα+Gk_CA^Bα=0，因为α，Aα，A^Bα线性无关，故

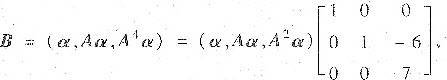
所以，α，Aα，A^Dα线性无关，因而矩阵B可逆.

(Ⅱ)因为(B^TB)^T=B^T(B)^T=B^TB，故B^TB是对称矩阵，又

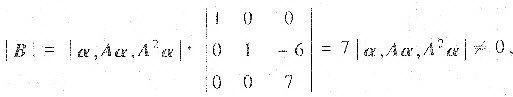，由于矩阵B可逆，恒有Bx≠0，那么恒有x^T(B^TB)x=(Bx)^T(Bx)＞0，故二次型x^T(B^TB)x是正定二次型，从而矩阵B^TB是正定矩阵.

解析：

①由

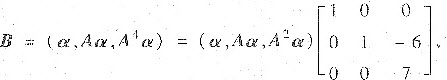
易知

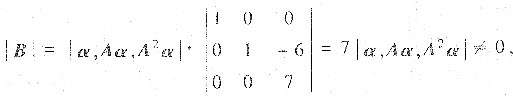亦可证得B可逆.

②正定矩阵是由二次型引出的，二次型矩阵A是实对称矩阵，因此若要证明A是正定矩阵，应先验证A是对称矩阵.

③要会用定义法证明正定，要熟悉向理的内积：(α，β)=a₁b₁+a₂b₂+…+a_nb_n=α^Tβ，特别地

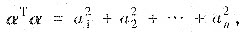那么