问题
填空题
设y(x)在(-∞,+∞)连续,又当Δx→0时α是比Δx高阶的无穷小,函数y(x)在任意点处的增量Δy=y(x+Δx)-y(x)满足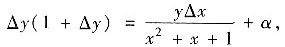
且y(0)=π,则y(1)=().
答案
参考答案:

解析:
[分析一] 先求y(x),再求y(1). 为求y(x)先求y′(x). 将已知等式两边同除Δx,并令
Δx→0,由连续性知
 于是取极限得
于是取极限得

这是可分离变量的微分方程,分离变量得

积分得
 ,即
,即

再由

[分析二] 将已知等式改写成

(因为
 ,记
,记
 ,则其中
,则其中
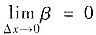 ,而且
,而且
 o(Δx)(Δx→0)),由Δy与微分dy的关系知,函数y(x)在任意点x处的微分为
o(Δx)(Δx→0)),由Δy与微分dy的关系知,函数y(x)在任意点x处的微分为

其余解法同[分析一].
设y=y(x)满足:
Δy=y(x+Δx)-y(x)=f(x,y)Δx+α (*)
其中α=o(Δx)(Δx→0),则

因此,(*)式是由自变量的增量与因变量的增量之间的关系给出的方程式. 本题就是这种情形的一个例子.
