问题
单项选择题
下列等式或不等式
①

②
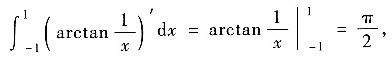
③设
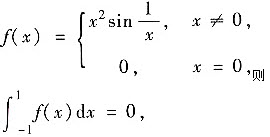
④
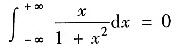
中正确的共有()
A.1个
B.2个
C.3个
D.4个
答案
参考答案:B
解析:
要逐一分析,
对于①:由
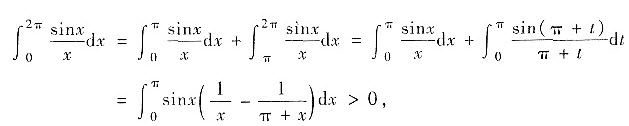
可知①正确.
对于②:因为
 在点x=0处无定义,不能在[-1,1]上用牛顿-莱布尼兹公式,因此②不正确. 事实上
在点x=0处无定义,不能在[-1,1]上用牛顿-莱布尼兹公式,因此②不正确. 事实上
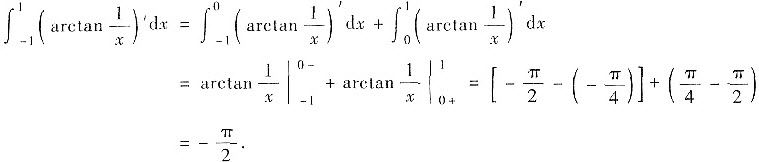
或由于
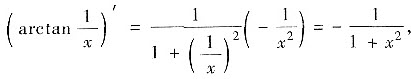 因此
因此
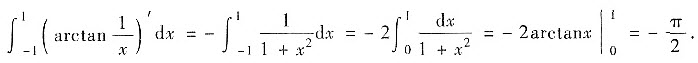
对于③:易知
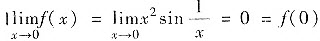 ,故f(x)在[-1,1]上连续,且是奇函数
,故f(x)在[-1,1]上连续,且是奇函数
 .
.
故③正确.
对于④:这里
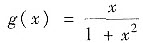 在(-∞,+∞)连续,虽是奇函数,但
在(-∞,+∞)连续,虽是奇函数,但
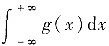 发散,因为
发散,因为

故④不正确,
综上分析,应选B.
若
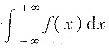 收敛,则
收敛,则
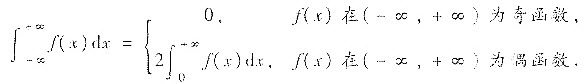
对瑕积分有类似结论.
