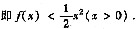问题
问答题
设函数f(x)在[0，+∞)内二阶可导，且f(0)=f’(0)=0，并当x＞0时满足
xf’’(x)+3x[f’(x)]2≤1-e-x.
求证：
答案
参考答案：
解析： 由泰勒公式得
( *)
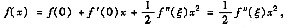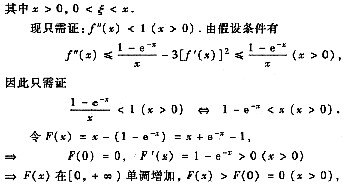
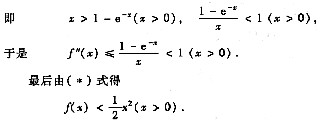
[分析与证明二]
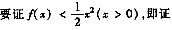
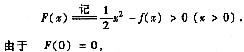
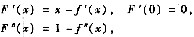
因此为证(* *)式，只需证1-f’’(x)＞0(x＞0)，即f’’(x)＜1(x＞0)．
现如同前面所证f’’(x)＜1(x＞0)，于是F’’(x)=1-f’’(x)＞0(x＞0)
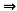F’(x)在[0，+∞)单调增加
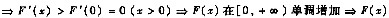＞F(0)=0(x＞0)，
