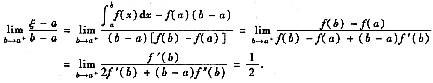问题
问答题
设f(x)在[a，b]上有二阶导数，且f(x)＞0．
(Ⅰ)证明至少存在一点ζ∈[a，b]，使
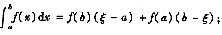
(Ⅱ)对(Ⅰ)中的ζ∈[a，b]，求
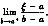
答案
参考答案：
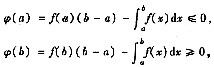
故由闭区间上连续函数的性质知存在ξ ∈[a，b]，使得φ(ξ)=0，即
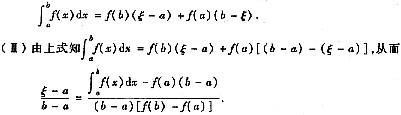
于是将b看作变量，分别对右端分式两次应用洛必达法则即得
搜题请搜索小程序“爱下问搜题”
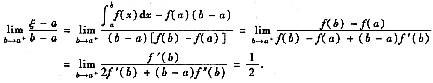
设f(x)在[a，b]上有二阶导数，且f(x)＞0．
(Ⅰ)证明至少存在一点ζ∈[a，b]，使
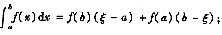
(Ⅱ)对(Ⅰ)中的ζ∈[a，b]，求
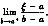
参考答案：
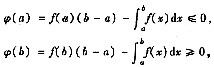
故由闭区间上连续函数的性质知存在ξ ∈[a，b]，使得φ(ξ)=0，即
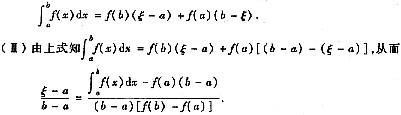
于是将b看作变量，分别对右端分式两次应用洛必达法则即得