问题
解答题
设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率.
答案
0.94 0.44
解:设Ak表示“第k人命中目标”,k=1,2,3.
这里,A1,A2,A3独立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
从而,至少有一人命中目标的概率为1-P(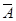 1·
1·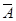 2·
2·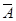 3)=1-P(
3)=1-P(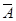 1)P(
1)P(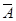 2)P(
2)P(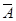 3)=1-0.3×0.4×0.5=0.94.
3)=1-0.3×0.4×0.5=0.94.
恰有两人命中目标的概率为
P(A1·A2·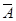 3+A1·
3+A1·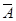 2·A3+
2·A3+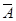 1·A2·A3)
1·A2·A3)
=P(A1·A2·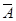 3)+P(A1·
3)+P(A1·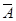 2·A3)+P(
2·A3)+P(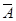 1·A2·A3)
1·A2·A3)
=P(A1)P(A2)P(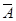 3)+P(A1)P(
3)+P(A1)P(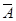 2)P(A3)+
2)P(A3)+
P(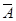 1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
∴至少有一人命中目标的概率为0.94,恰有两人命中目标的概率为0.44.
