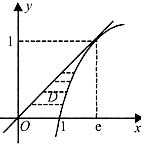
过坐标原点作曲线．y=lnx的切线，该切线与曲线y=lnx及x轴围成平面图形D．
(1)求D的面积A；
(2)求D绕直线x=e旋转一周所得旋转体的体积V．
参考答案：
[分析]： 先求出切点坐标及切线方程，再用定积分求面积A；旋转体体积可用一大立体(圆锥)体积减去一小立体体积进行计算，为了帮助理解，可画一草图．
[解] (1)设切点的横坐标为x0，则曲线y=lnx在点(x0，lnx0)处的切线方程是
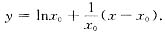
由该切线过原点知lnx0-1=0，从而X0=e．所以该切线的方程为
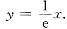
平面图形D的面积
(2)切线
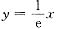与x轴及直线x=e所围成的三角形绕直线x=e旋转所得的圆锥体积为
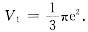
曲线y=lnx与x轴及直线x=e所围成的图形绕直线x=e旋转所得的旋转体体积为
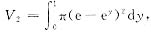
因此所求旋转体的体积为
[评注] 本题不是求绕坐标轴旋转的体积，因此不能直接套用现有公式．也可考虑用微元法分析．
请结合下列在展览会上摘选材料与所学知识回答：（18分）
展览一：公元前六世纪—公元前五
世纪中西文明的对照
展览二：19世纪中后期的中国存在对西学的争论
甲认为中国是文明古国，周围国家是蛮夷禽兽之国，文化落后，因此，只能是以夏变夷，从来没有听说过“以夷变夏”。
乙认为中国擅长的是道，西方擅长的是器。中国原来也包括器的，但是后来这套科学技术“器”的研究没有被重视，失传了，传到西方去了。我们现在向西方学习，学的即是我们传过去的东西，中国古已有之，传到西方，现在“天将器还中国”，我们又学习，这是合理的，必要的。
丙认为乙是在“古书中猎取近似陈言，谓西学皆中土所已有，并无新奇”，其意在“扬己抑人”。这种“西学中源说”的一大危害是造成社会更加崇古，“必谓事事
必古之从，又常以不及古为恨”，以致在西学问题上只重器，而不能从更广泛的层面上进行学习。
（1）下表是展览中对体现当时中西文明重要成果的人物的介绍，请参考已填充的文字，完成空白部分。（9分）
| 人名 项目 | 中国孔子 | 古希腊亚里士多德 |
| 时代 特征 | 奴隶制社会向封建制社会转型；礼崩乐坏；百家争鸣。 | |
| 思想 观点 | 求知是人类的本性；人是理性政治动物； 人是天生的政治动物等。 | |
| 地位 | 成为中国传统文化的主流。其博大的精神文化品格，在世界文化史上具有重要影响。孔子被尊称为圣人 |
