某项目投资值服从三角形分布，对投资值的三角形分布向专家调查最

问题问答题

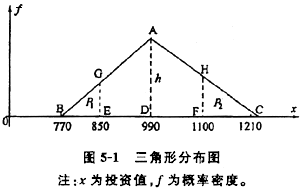
某项目投资值服从三角形分布，对投资值的三角形分布向专家调查最可能值、悲观值和乐观值。调查结果扣表5-2所示。
表5-2 单位：万元

问题：
(1)计算投资悲观值、最可能值、乐观值的平均值、方差、标准差、离散系数。
(2)计算实际投资值为850万元以下或1100万元以上的概率。
(3)如果利用蒙特卡罗模拟方法，利用随机数对应累积概率的方法，在上述条件下如果抽得随机数为40000，利用线性插值法确定其对应的投资值。

答案

参考答案：

解析：：
平均值

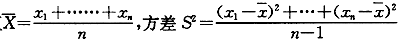,标准差为S，离散系数

。
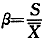悲观值

同理得到表5-7。
表5-7

因此，产品产量服从乐观估计为1210万元、最可能值为990万元、悲观值为770万元的三角形分布：相应的离散系数分别为12.3%、11.1%和11.5%。
问题(2)：

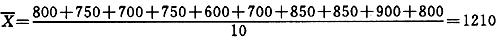
根据概率理论基本知识可知：
因为

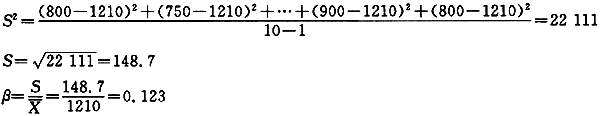
所以

因为
所以

因为

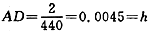
所以

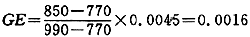
实际投资值为850万元以下的概率为0.064，实际投资值超过1100万元的概率为0.1。

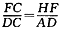
问题(3)：

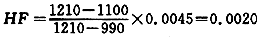
随机数为40 000时设累积概率为0.4，根据线性插值公式可得到下式：

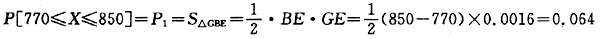
∴X_o＝880.86(万元)
∴随机数为40000时对应的投资值为880.86万元。