问题
问答题
设二维随机变量(X，Y)的概率密度为
f(x，y)=Ae-2x2+2xy-y2，-∞＜x＜+∞，-∞＜y＜+∞，
求常数A及条件概率密度fY|X(y|x)．
答案
参考答案：[解] 方法一 常数A可以通过性质
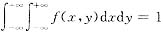来求．
而
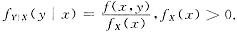
其中
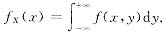
其实^(z)中带有常数A，所以用
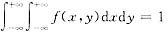来求A，还不如用
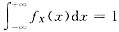来求A
所以先求
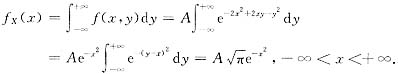
又由于
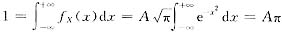，即
．
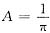当fx(x)＞0时，等价于当-∞＜z＜∞时，
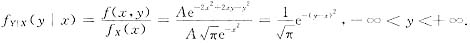
[评注] 这方法中用了公式
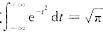，此公式可以从服从正态
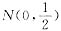的密度函数
的积分等于1来推出．
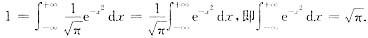
方法二 二维正态概率密度一般形式为
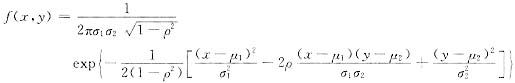
对比本题所给二维密度f(x，y)=Ae-2x2+2xy-y2，可知μ1=μ2=0，且
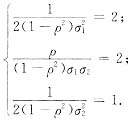
由此解得
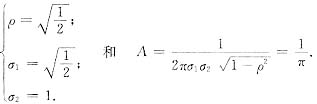
这时的边缘密度
．
，
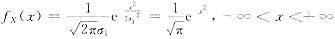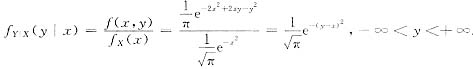