问题
问答题
一完全垄断厂商的需求函数为Q=1 000-5P，成本函数为TC=200-2Q+5Q2。
(1)从厂商追求最大利润的角度，应确定的价格和产出为多少
(2)如果政府决定实行价格管制，按照平均成本定价，价格为多少
(3)如果按照边际成本定价，价格为多少厂商是否亏损，政府补贴多少才能使完全垄断厂商保本
答案
参考答案：
解析：(1)根据需求函数可知P=200-0.2Q，总收益函数为TR=P·Q=200Q-0.2Q2，由此可得边际收益函数为MR=200-0.4Q；边际成本函数MC=dTC/dQ=-2+10Q。
根据利润最大化原则MR=MC，即200-0.4Q=-2+10Q，解得Q=19.42，P=200-0.2Q=196.12元。
(2)如果政府实行价格管制并按平均成本定价，则价格为P=ATC=(
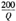-2+5Q=200-0.2Q，从而得到方程5.2Q2-202Q+200=0解得Q=37.83，P=200-0.2Q=200-0.2×37.83=192.43。
(3)如果按边际成本定价，P=MC=-2Q+10Q=200-0.2Q解得Q=19.8，P=200-0.2Q=196.04元。
利润π=TR-TC=P·Q-200+2Q-5Q2=196.04×19.8-200+2×19.82=1 760.99元＞0
因此，厂商不会发生亏损，不需要政府补贴。