甲公司计划开发一种高科技的新产品,相关资料如下:
(1)项目的投资成本为190万元。
(2)预期项目可以产生平均每年20万元的永续现金流量;该产品的市场有较大的不确定性。如果消费需求量较大,营业现金流量为25万元;如果消费需求量较小,营业现金流量为15万元。
(3)如果延期执行该项目,一年后则可以判断市场对该产品的需求,并做出取舍。
(4)等风险投资需求的报酬率为10%,无风险的报酬率为5%。
要求:

(1)计算不考虑期权的项目净现值。
(2)采用二叉树方法计算延迟决策的期权价值(请将结果填入“期权价值计算表”中),并判断应否延迟执行该项目。
参考答案:
(1)项目净现值=20÷10%-190=10(万元)
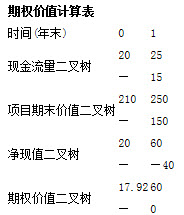
(2)①项目价值二叉树
上行项目价值=上行现金流量÷折现率=25÷10%=250(万元)
下行项目价值=下行现金流量÷折现率=15÷10%=150(万元)
②项目净现值二叉树
上行项目净现值=上行项目价值-投资成本=250-190=60(万元)
下行项目净现值=下行项目价值-投资成本=150-190=-40(万元)
由此可知,期权价值为0,应当放弃。
③期权价值二叉树
1年末上行期权价值=项目净现值=60(元)
1年末下行期权价值=0
上行报酬率=(本年上行现金流量+上行期末价值)÷年初投资-1=(25+250)÷190-1=44.74%
下行报酬率=(本年下行现金流量+下行期末价值)÷年初投资-1=(15+150)÷190-1=-13.16%
无风险利率=5%=上行概率×44.74%+(1-上行概率)×(-13.16%)
上行概率=0.3136
下行概率=1-0.3136=0.6864
期权到期日价值=上行概率×上行期权到期价值+下行概率×下行期权到期价值=0.3136×60+0.6864×0=18.82(元)
期权的现行价值=18.82÷(1+5%)=17.92(元)