某上市公司计划投资一个新项目，分两期进行，第一期在2009年1月1日投资，投资合计为1000万元，经营期限为10年，预计每年的税后现金流量为150万元；第二期项目计划于2012年1月1日投资，投资合计为2000万元，经营期限为8年，预计每年的税后现金流量为400万元。公司的既定最低报酬率为10%。无风险的报酬率为4%，项目现金流量的标准差为20%。
已知：(P/A，10%，10)=6.1446，(P/A，10%，8)=5.3349
(P/F，10%，3)=0.7513，(P/F，4%，3)=0.8890
N(0.13)=0.5517，N(0.12)=0.5478
N(0.47)=0.6808，N(0.48)=0.6844
要求：
(1)计算不考虑期权的第一期项目的净现值。
(2)计算不考虑期权的第二期项目在2012年1月1日和2009年1月1日的净现值。
(3)如果考虑期权，判断属于看涨期权还是看跌期权；确定标的资产在2012年1月1日的价格和执行价格，并判断是否应该执行该期权。
(4)采用布莱克—斯科尔斯期权定价模型计算考虑期权的第一期项目的净现值，并评价是否应该投资第一期项目。
参考答案：
(1)不考虑期权的第一期项目的净现值=150×(P/A，10%，10)-1000=-78.31(万元)
(2)不考虑期权的第二期项目在2012年1月1日的净现值=400×(P/A，10%，8)-2000=133.96(万元)
不考虑期权的第二期项目在2009年1月1日的净现值=400×(P/A，10%，8)×(P/F，10%，3)-2000×(P/F，4%，3)=-174.76(万元)
(3)从题意可知这是一项到期时间为3年的看涨期权，如果标的的资产在2012年1月1日的价格高于执行价格，则会选择执行期权。标的资产在2012年1月1日的价格=400×(P/A，10%，8)=2133.96(万元)，标的资产在2012年1月1日的执行价格=投资额=2000(万元)，由于2133.96大于2000，因此，会选择执行该期权。
(4)S0=400×(P/A，10%，8)×(P/F，10%，3)=1603.24(万元)
PV(X)=2000×(P/F，4%，3)=1778(万元)
d1=In(1603.24÷1778)÷(0.20×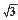
)+(0.20×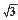)÷2=-0.1035÷0.3464+0.1732=-0.1256
d2=-0.1256-0.3464=-0.472
N(d1)=1-N(0.1256)=1-[0.5478+(0.5517-0.5478)÷(0.13-0.12)×(0.1256-0.12)]=0.4500
N(d2)=1-N(0.472)=1-[0.6808+(0.6844-0.6808)÷(0.48-0.48)×(0.472-0.47)]=0.3192
C0=1603.24×0.4500-1778×0.3192=721.46-567.54=153.92(万元)
考虑期权的第一期项目净现值=153.92-78.31=75.61(万元)，因此，可以投资第一期项目。