问题
问答题
设f"(x)∈C[a,b],证明:存在ζ∈(a,b),使得
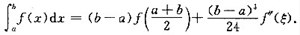
答案
参考答案:
[*]
因为f(x)∈C[a,b],所以f(x)∈C[ζ1,ζ2],由闭区间上连续函数最值定理,f"(x)在区间[ζ1,ζ2]上取得最小值和最大值,分别记为m,M,则有
[*]
再由闭区间上连续函数的介值定理,存在ζ∈[ζ1,ζ2][*](a,b),使得f"(ζ)=
[*]
设f"(x)∈C[a,b],证明:存在ζ∈(a,b),使得
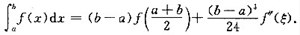
参考答案:
[*]
因为f(x)∈C[a,b],所以f(x)∈C[ζ1,ζ2],由闭区间上连续函数最值定理,f"(x)在区间[ζ1,ζ2]上取得最小值和最大值,分别记为m,M,则有
[*]
再由闭区间上连续函数的介值定理,存在ζ∈[ζ1,ζ2][*](a,b),使得f"(ζ)=
[*]