问题
问答题
设f(x)可导，x∈(-∞，+∞)，
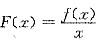在x=1处取得极值，试证：曲线y=f(x)在x=1处的切线通过原点．
答案
参考答案：曲线y=f(x)在点(1，f(1))处的切线方程为
y-f(1)=f’(1)(x-1)
由
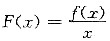在x-1处取得极值，知F’(1)=0．
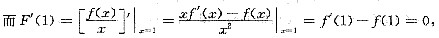
即f’(1)=f(1)．
故切线方程为
y-f(1)=f(1)(x-1)，
即y=f(1)x．
这就说明，该切线通过原点．
解析：
[分析]： 利用可导函数取得极值的必要条件．