问题
问答题
证明：当x≥0时，x≥arctanx。
答案
参考答案：
令f(x)=x-arctanx，则
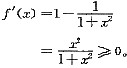
从而知y=f(x)为单调增加函数。
由于f(0)=0，可知当x≥0时有f(x)≥f(0)。故当x≥0时有
x≥arctanx。
搜题请搜索小程序“爱下问搜题”
证明：当x≥0时，x≥arctanx。
参考答案：
令f(x)=x-arctanx，则
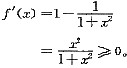
从而知y=f(x)为单调增加函数。
由于f(0)=0，可知当x≥0时有f(x)≥f(0)。故当x≥0时有
x≥arctanx。