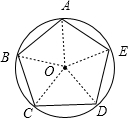
证明：设圆内接五边形为ABCDE，圆心是 O．

连接OA，OB，OC OD，OE，可得五个三角形

∵OA=OB=OC=OD=OE=半径，∴有五个等腰三角形

在△OAB、△OBC、△OCD、△ODE、△OEA中

则∠OAB=∠OBA，∠OBC=∠OCB，∠OCD=∠ODC，∠ODE=∠OED，∠OEA=∠OAE

因为所有内角相等，

所以∠OAE+∠OAB=∠OBA+∠OBC，所以∠OAE=∠OBC

同理证明∠OBA=∠OCD，∠OCB=∠OED，∠ODC=∠OEA，∠OED=∠OAB

则△OAB、△OBC、△OCD、△ODE、△OEA 中，∠AOB=∠BOC=∠COD=∠DOE=∠EOA

∴△OAB≌△OBC≌△OCD≌△ODE≌△OEA  （SAS边角边定律）

∴AB=BC=CD=DE=EA

∴五边形ABCDE为正五边形