问题
问答题
假设总体Xi(i=1,2)服从正态分布
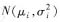 ,X1和X2相互独立,由来自总体Xi(i=1,2)的简单随机样本得样本均值
,X1和X2相互独立,由来自总体Xi(i=1,2)的简单随机样本得样本均值
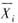 和样本方差
和样本方差
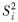 .
.
利用正态总体的样本均值和样本方差的性质,证明:
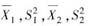 相互独立;
相互独立;
答案
参考答案:由于[*]分别依赖于两个相互独立的样本,故它们相互独立.由于正态总体的样本均值和样本方差相互独立,可见[*]分别相互独立.因此,对于任意实数a,b,c,d,有
[*]
从而[*]相互独立.
假设总体Xi(i=1,2)服从正态分布
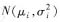 ,X1和X2相互独立,由来自总体Xi(i=1,2)的简单随机样本得样本均值
,X1和X2相互独立,由来自总体Xi(i=1,2)的简单随机样本得样本均值
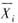 和样本方差
和样本方差
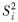 .
.
利用正态总体的样本均值和样本方差的性质,证明:
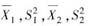 相互独立;
相互独立;
参考答案:由于[*]分别依赖于两个相互独立的样本,故它们相互独立.由于正态总体的样本均值和样本方差相互独立,可见[*]分别相互独立.因此,对于任意实数a,b,c,d,有
[*]
从而[*]相互独立.