阅读下面的文字,完成(1)一(4)题。
你要是到村子里去打听九公,无论大人小孩几乎没有不知道的。九公是全村年龄最长、辈分最高的老人,是远近有名的有趣人,他的趣事就如同他的胡须,多地数也数不清。
九公九岁的时候,被送去读私塾。九公对那些摇头晃脑的“子乎者也”十分烦感。先生也不喜欢这个调皮的学生,时不时出一些难题难为他。一天在讲曹植七岁成诗时,九公却和周公秘密会谈去了。先生十分生气,就让九公当场作诗一首,不然就挨板子。九公望着窗外的瓢泼大雨,歪着头,略作思索,遂以《雨》成诗。
盆泼也
瓢倒也
一滴雨
一个大豆也
全班同学笑成一团,先生气得差点背过气去。
九公的学业也就到此结束了。
“扫盲”的那几年,九公也和大伙一起去村小学学习。那节语文课,老师教学“人”字,九公再次拜会周公,呼呼大睡。老师辈分低,既要严肃课堂纪律,又要给爷爷辈的九公脸面,便耐心地开导他。 “其实汉字很容易学,一人为“人”,二人为“从”,是说两人在一起,三人为“众”,是说很多人的意思——多形象!多生动!”
九公走上讲台,边说边在黑板上写。
“如果人上边有人,人下边也有人,人左边也有人,人右边也有人,人加人,人叠人,人连人,念什么字?”九公在黑板上写了密密麻麻、歪歪扭扭七八个“人”字。
老师有点生气。“这不是字!”
“不是字?”九公面向大伙,手一挥,如同一位镇定自若的 * * 。“这个字念——一堆人!”
从去年入冬以来,天气持续干旱,许多地方遭遇五十年一遇的干旱袭击,大片大片的庄稼开始枯黄。我们这里也不例外,大伙开始忙着抗旱保收。但是由于基础设施匮乏,加之抗旱又是个费时费力的活儿,所以效果不明显。人人都是看在眼里,急在心里。
这时,九公做了一件惊天动地的大事。
那天,九公带领四个六七十岁的老伙计来到河边求雨。九公说,河中心有个千年鳖精,呼风唤雨,无所不能。他年轻时曾见过有人在这里求雨,当天就电闪雷鸣,大雨倾盆。方圆几里、四面八方的人都赶来看热闹。
九公在河边支起一个供案,上面摆着供品,然后点燃三柱香,双手捧着擎过头顶,对着上天三叩九拜,口中还念念有词,不知说些什么。
之后,真正的求雨过程开始了。
九公身背一个簸箕——此时他就是是千年鳖精的化身。四个帮手分列东南西北,围成一个圈,每人手中还提着一壶水。
九公就在中间爬来爬去。爬到东面,就抬头问:“东海龙王下不下雨?”帮手忙说:“有雨!”提起壶在九公身上浇一阵。爬到西面,九公又问:“西海龙王下不雨?”西面的帮手忙说:“有雨!”提起壶在九公身上又浇了一阵子。“南海龙王”“北海龙王”也都声称:有雨!九公就这样爬来爬去,衣服渐渐湿透了。
说来也怪,天真是渐渐地阴沉下来,起风了。甚至还滴下几滴雨来。
轰隆隆,轰隆隆!
一阵响过一阵,一阵急过一阵的巨响在天空回荡。
“打雷了!要下雨了!老天爷显灵啦!”九公激动地老泪纵横。“都别傻站了,快跪下来求老天爷吧!”九公向周围的人群喊去。有两个老太太当即就跪下了。
就在众人不知所措的时候,村支书刘义气喘吁吁地跑过来。“别瞎闹啦!部队趁着今天的有利天气正在人工降雨呢。炮弹已经打过了,马上就要下雨。谁要是不想饿肚子,就赶快去地里挖沟引水,我只通知这一次啊!”刘义说完又转头跑掉了。
人群一哄而散。九公慌忙喊:“哎!别走!哎!”九公的四个帮手最后也随着人流不见了。 九公一下子瘫坐地上。
雨足足下了一天一夜。雨过天晴,天空升起一道美丽的彩虹。
从此,九公就常常坐在村头的那棵大柳树下,对着那些 背着书包上学的小学生,不厌其烦地说:“娃呀,好好读书。将来有知识才能长本事!”
(1)下列对小说有关内容的分析和概括,最恰当的两项是( )
A.九公不识字,从小对“之乎者也”之类的私塾教育就非常反感,这说明九公的性格中具有一定的叛逆性和反封建性。
B.参加扫盲学习时,九公不但再次拜会“周公”,而且还倚杖辈分当堂捣乱,这样描写既照应了上文,也突出了九公不尊重知识的思想根深蒂固。
C.这篇小说主要是通过语育描写和动作描写来刻画人物形象,语言生动诙谐,洋溢着浓郁的生活气息。 D.九公求雨之后,天色的确变得阴沉,继而雷声轰隆,说明九公求雨还是有一定效果的,但最后一天一夜的透雨靠的还是部队利用天气条件进行的人工降雨技术。
E.接到村支书通知后,人们一哄而散纷纷回地里挖沟引水,连九公的四个帮手也随着人流不见了,小说这样描写隐含着对人们势利自私的委婉批评。
(2)小说中的九公是一个什么样的形象?请简要分析。
__________________________________________________________
(3)小说详细描写了九公“求雨”的过程,请分析其作用。
__________________________________________________________
(4)有人认为这篇小说的最后一段画蛇添足,有人却认为此结尾画龙点睛,你怎么看呢?结合全文,谈谈你的观点和理由。
__________________________________________________________
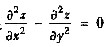 ,若有z(x,2x)=x,z’1(x,2x)=z’x(x,y)|y-2x=x2,求z"11(x,2x)与z"12(x,2x).
,若有z(x,2x)=x,z’1(x,2x)=z’x(x,y)|y-2x=x2,求z"11(x,2x)与z"12(x,2x).