问题
问答题
设函数f(x)，g(x)在[a，b]上连续，在(a，b)内可导，且g’(x)≠0(
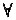x∈(a，b))，求证：若
单调增加，则
在(a，b)单调增加．
答案
参考答案：不妨设g’(x)＞0(x∈(a，b))，考察
[*]
=[*](柯西中值公式，其中ξ∈(a，x))，由g’(x)＞0(x∈(a，b))，g(x)在[a，b]连续[*]g(x)-g(a)＞0(x∈(a，b))．由[*]在(a，b)单调增加[*]，因此[*]，即[*]在(a，b)单调增加．
